Definição e Fórmula
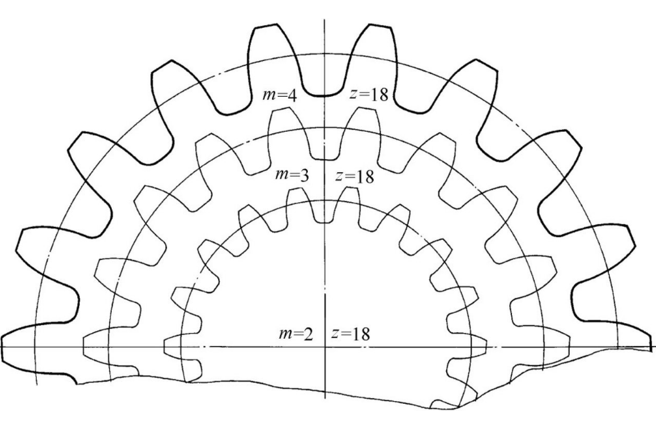
Omódulo de engrenagemé um parâmetro fundamental no projeto de engrenagens que define o tamanho dos dentes da engrenagem. É calculado como a razão entrepasso circular(a distância entre pontos correspondentes em dentes adjacentes ao longo do círculo primitivo) para a constante matemáticaπ (pi). O módulo é normalmente expresso em milímetros (mm).

Onde:
● m = módulo de engrenagem
● cp = passo circular
Principais funções do módulo de engrenagens
1. Padronização:
O módulo padroniza as dimensões das engrenagens, permitindo compatibilidade, intercambiabilidade e facilidade de produção em massa.
2. Determinação da força:
O módulo afeta diretamente a espessura e a resistência dos dentes da engrenagem. Um módulo maior resulta em dentes mais fortes, capazes de suportar cargas maiores.
3. Influência dimensional:
Ela influencia dimensões críticas de engrenagens, comodiâmetro externo, altura do dente, ediâmetro da raiz.
Critérios de seleção de módulos
●Requisitos de carga:
Cargas mecânicas mais altas exigem um módulo maior para garantir resistência e durabilidade adequadas.
●Considerações sobre velocidade:
Para aplicações de alta velocidade, ummódulo menoré preferível para minimizar as forças inerciais e reduzir o ruído.
●Restrições de espaço:
● Em projetos compactos ou com espaço limitado, ummódulo menorpermite redução do tamanho geral da engrenagem, mantendo a funcionalidade.
Tamanhos de módulos padrão
Os valores comuns de módulos padronizados incluem:
0,5, 0,8, 1, 1,25, 1,5, 2, 2,5, 3, 4, 5, 6, 8, 10, 12, 16, 20, 25, 32, 40, 50, etc.
Exemplo de cálculo
Se o passo circular cpcpcp for6,28 milímetros, o módulo de engrenagem mmm é calculado como:
m=6,28π≈2 mmm = \frac{6,28}{\pi} \aprox 2\ \text{mm}m=π6,28≈2 mm
Resumo
O módulo de engrenagem é um parâmetro de projeto crucial que afeta atamanho, força, edesempenhode uma engrenagem. A seleção do módulo apropriado garante funcionalidade, confiabilidade e compatibilidade ideais com base nas demandas específicas da aplicação, incluindo limitações de carga, velocidade e espaço.
Horário de publicação: 09/05/2025